前言
如果你想去更大的平台发展,比如微软、阿里、Airbnb、亚马逊,即使是前端的岗位,在面试时(甚至每一轮)也会考验一些算法题目(虽然我觉得没什么道理)。总的来说面试算法题的公司一半一半吧,另一半倾向于面试前端相关的实战练习题。外企基本不考察你的前端能力,只考虑你的算法和数据结构能力(别问我是怎么知道的,我的面试史就是一部血泪史)。所以前端同学懂一些基本的算法也是有必要的。我不知道其他语言的程序员在找工作时面试的算法题有哪些,但前端的算法面试题还算是比较基础并且不难(至少相对于我而言)。我也算是面霸了,所以分享一些个人经验,同时也是记录下来写给将来的有需要的自己。
中间还会穿插两道实战题,以及强调一些概念。
送分题不能丢
你常常有听到说面试前刷 leetcode 的说法。但是在刷 leetcode 题目之前,我认为有些基础分必须拿到,或者说送分题必须不能丢。
什么是送分题?就是你大学数据结构或者是C语言教材遇到的那些题目。这些题目你做过,花一个学期学习过,即使现在忘了捡起来也算是容易的。例如数据结构里的那些排序算法,查找算法,还有树的相关知识。面试的题目相对于书的内容其实更窄,比如关于树的知识点,面试官的题目可能会暗示你是用二叉树去解决一个问题,或者计算叶子节点个数,或者计算树的深度。其他更简单的例如使用递归和非递归的方式写出二叉树的前中后序遍历。并不会考到例如平衡二叉树或者是完全二叉树的这样的概念(至少我没有遇到过),更不要说图这样的概念了。
查找算法遇见的不多,更多的是考察排序算法。算法的基本款是必须要掌握的:冒泡排序、选择排序、插入排序、快速排序、归并排序、桶排序。学会写这些算法是下策,上策是你要知道这些算法的原理和效率(也就是时间复杂度)。比如当你在面试里卡壳的时候,你至少可以描述算法是如何工作的。而之所以要了解它们的效率,是因为面试官有可能让你间接的写一个算法,例如不考虑空间效率,写一个时间效率最高的。学会判断时间复杂度很重要,在后面我们也会用到。
当你确保这些基础题都已经万无一失了。那么就可以开始尝试练习更难的题目了(抱歉我也不知道什么样才算更难得题目)。
当然难和容易依然是相对的,或许这些题目对我来说还算是简单,但是一部分人来说仍然困难。但无论如何都有你擅长和曾经遇到过的问题,稳扎稳打,这些送分题不能丢。
对算法精益求精
我高中数学老师曾经教导我们考试的最高境界是揣摩出出题者的意图。每一位面试官提出的问题,其实在他心里都已经有一个最佳答案了。所以面试的最高境界也是要击中面试官心中的那个最优解,至少算法题这一块必须如此,当然你要是有更好的解决方案会更棒。
当一道算法题给出时,你要想的不仅仅是如何解决这个问题,并且是如何最好的解决这个问题(如果时间允许的话你可以写两个解法)。然而怎样算更优的解呢,当然是更高效,时间复杂度更低的方案。
接下来我们先粗略的说一说如何计算时间复杂度,以及通过实例说明什么是更优的方案。
计算时间复杂度
时间复杂度是衡量一个算法快慢的标志(当然也存在空间复杂度)。时间复杂度说白了就是语句的执行次数,但这个执行次数我们要从抽象和宏观的角度去考虑。
例如你写了一段十行的代码,但代码语句不一定只执行了十条,因为其中可能有一条语句需要循环执行N次。当这个N等于10或20时,循环执行对于性能开销微乎其微,但如果N变成百万或者千万级别的,性能的开销就很可观了。更甚者,如果这10行代码中有一条语句是被N次嵌套循环执行,那么执行的次数就是N*N = N^2,如果此时N依旧是百万或者千万级别,那么后果就可想而知了。
通过以上的实例可以看出,一段代码执行速度的瓶颈其实在于循环语句的执行效率(次数),所以当需要计算一段代码的时间复杂度时,我们着重把代码中影响最大的循环部分抽取出来,统计它的执行次数即可。时间复杂度用大O(Big O notion)表示。常见的时间复杂度情况有以下几种
- 常数(Constant Time)级别
O(1):当执行代码中不存在循环语句时时间复杂度即为常数级别,值得一提的是此时即使你的代码有上百行也算是这个级别的,因为相对于循环中无限可能的N来说不值一提; - 线性(Linear Time)级别
O(n):即一层嵌套循环,最常见的操作就是遍历数组,查找最小值什么的; - 对数(Logarithmic Time)级别
O(logN): 即执行次数是N的一半,例如在一个有序的数组中做折半查找、或者是二叉树搜索:
while ( low <= high ) {
mid = ( low + high ) / 2;
if ( target < list[mid] )
high = mid - 1;
else if ( target > list[mid] )
low = mid + 1;
else break;
}
- 平方数(Quadratic Time)级别
O(n^2),执行次数是N的平方,也就是我们最常见的两层嵌套循环。这种场景在接下来的冒泡排序或者选择排序中都能看到
以上是常见的一些复杂度级别,基于以上的认知,还可以推断出当代码中有c层嵌套循环时,时间复杂度可以是指数级别O(n^c);又例如代码有有一层循环执行,但每层循环执行中又有一个折半查找,那么这段代码的时间复杂度就是一个组合情况O(N * logN)。
你可能存在的另一个疑问是,如果在计算时间复杂度时不加上其他语句执行的次数,这样岂不是更精确。例如一段一百行的代码,其中有三行负责的是N次循环的语句,其余的97行都是非循环语句,那么时间复杂度可以是O(N + 97)?
这么说没有错,但这么做大可不必,因为常量对N的影响微乎其微。想象当N增长到百万级别时,常量(无论是成百还是上千)在N、logN、N^2前都显得太渺小,也就是说,这个算法效率差的本质其实是 N本身以及它的循环次数决定的,增加或者减少一个常量并不会让它执行变得更快或者更慢。所以通常在描述算法是都会撇弃常量。
在某些场景中,例如排序算法,循环的执行次数可能还与初始化等待排序的数组次序有关。所以还要区分最好情况和最坏情况的时间复杂度,这个问题具体情况具体分析。
更优解实战
基于上面的知识点,我们用一道题实战一下。题目如下:
给出任何一个字符串,比如sdjkasbfknmsdlasdhjbbmrtuy,找出第一次出现(从左至右顺序)的,且在字符串里只出现过一次的字符。
首先我们怼上暴力解法,即依次遍历:
function find(str) {
for (var i = 0; i < str.length; i++) {
var count = 0;
var flag = true;
for (var j = 0; j < str.length; j++) {
if (str[i] === str[j]) {
count++;
}
if (count > 1) {
flag = false;
break;
}
}
if (flag) {
return str[i];
}
}
}
这个方案有没有解决问题?有。但是不是最优解?不是,很显然它有两层循环嵌套,时间复杂度是O(n^2)。接下来我直接给出更优解,你们先看看是什么原理:
function find(str) {
var arr = new Array(str.length);
var characterMap = {};
var arrIndex = 0;
var finalIndex = -1;
for (var i = 0; i < str.length; i++) {
var char = str[i];
if (characterMap[char] == undefined) {
characterMap[char] = arrIndex++;
arr[characterMap[char]] = 1;
} else {
var index = characterMap[char];
arr[index]++;
}
}
for (var i = 0; i < arr.length; i++) {
if (arr[i] === 1) {
finalIndex = i;
break;
}
}
if (finalIndex !== -1) {
for (var key in characterMap) {
if (characterMap[key] === finalIndex) {
return key;
}
}
}
return;
}
如果只看代码里的循环的话,最多只存在三个循环,注意这三个循环是线性的,不是嵌套的,所以时间复杂度是O(3n),移除常量的话即是O(n)。
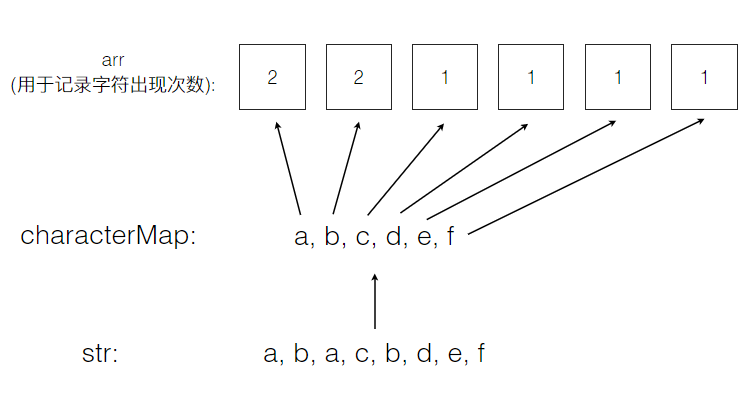
然而原理是什么?相信你也看出来了,就是用空间牺牲时间,和桶排序的原理相似。我们把字符串的每个字符分离出来,构造一个hash表,key就是字符,值即为一个数组的索引值,而数组则按照字符出现的顺序记录字符出现的次数。最后再遍历计数表,即能找到第一个只出现一次的字符。
原理如下图所示:
请同时考虑递归和非递归的解法
如果你在练习算法的过程中习惯使用递归算法,那么请同时考虑非递归算法如何实现。个人经验是通常使用递归算法实现的功能也会要求用非递归算法实现。为什么要使用非递归解法?因为如果数量级较大的话,递归解法会出现栈溢出的情况。接下来我举一个在实际面试中遇见的动态规划的例子。
比如我有下面代码中这种个数按照行数依次递增的数字三角形,寻找一条从顶部到底边的路径(即每行选取一个数),使得路径上所经过的数字之和最大。路径上的每一步都只能往左下右下走。只需要求出这个最大和即可,不必给出具体路径。
5,
6, 7,
9, 10, 3,
12, 23, 0, 20
8, 10, 11, 16, 8,
首先我们决定用二维数组的方式存储这类数据结构:
var arr = [
[5],
[6, 7],
[9, 10, 3],
[12, 23, 0, 20],
[8, 10, 11, 16, 8]
];
递归解法
- 例如我们要求从第1行到第2行的路径最大值,那么实际上只要从第二行中选一个最大值的然后加上第一行的就可以了;
- 如果需要求从第1行到第3行的路径最大值,那么原理其实也是找出第二行到第三行的路径最大值,然后加上第一行的值。那么如何求从第二行到第三行的最大值呢,可以利用上一步中的原理,找到6或7的最大值取较大值。
也就是说,想求a[i][j]的路径最大值,实际上是求a[i + 1][j]或a[i + 1][j + 1]两者中较大的路径最大值,取得后加上a[i][j]的值。而a[i + 1][j]和ar[i + 1][j + 1]路径最大值的求发与a[i][j]一致。这就形成了一个递归。而递归的终止条件则是a[i][j]已经是最后一行的元素了,或者a[i][j]不存在
function max(arr, i, j) {
if (arr[i][j] == undefined || i === arr.length - 1) {
return arr[i][j] || 0;
} else {
return arr[i][j] + Math.max(
max(arr, i + 1, j),
max(arr, i + 1, j + 1)
)
}
}
而非递归算法理解起来更简单。看最后两行:
[12, 23, 0, 20],
[8, 10, 11, 16, 8]
对于倒数第二行的第一个数12来说,最大路径只可能是12 + 8或者12 + 10;很明显最大值是12 + 10 = 22。此时为了节省空间,我们可以把最大值22覆盖原始值12. 同理,我们可以依次求出倒数第二行其他数值的最大路径值,最后结果是:
[22, 34, 16, 36]
[8, 10, 11, 16, 8]
同理,我们可以求出倒数第三行,倒数第四行每个数的最大路径值,直到第一行第一个数。实现如下:
function maxWithoutRecursion(arr) {
for (var i = arr.length - 2; i >= 0; i--) {
for (var j = 0; j < arr[i].length; j++) {
arr[i][j] = arr[i][j] + Math.max(
arr[i + 1][j],
arr[i + 1][j + 1] || 0
)
}
}
return arr[0][0]
}
结束语
关于算法面试我要分享的就这么多了。下次聊关于React面试中需要注意的地方。也欢迎留言补充。
参考文章
